
高光谱图像非监督分类方法
高光谱遥感技术起源于20世纪80年代初,它是在多光谱遥感技术的基础上发展起来的。经过数十年的发展,现在的高光谱遥感技术已经达到了一定的水平,在很多领域也得到了应用。比如它在农业中的应用,其主要表现在快速、精准地获取各种环境信息,以及农作物生长情况。在大气与环境应用上,在太阳光谱中,大气中的分子,如氧气、臭氧、二氧化碳、水蒸气等成分的反应十分强烈。而因为大气成份生变而引起的光谱差异通过传统宽波遥感方法难以准确识别,而这种差异可通过窄波段的高光谱识别出来。
非监督分类方法
1 K-means分类
K-means分类方法是最典型的目标函数聚类方法,以原型为依据。包含了以下流程:
1)从n个数据对象任意选择k个对象作为初始聚类中心(m1,m2,m3,…,mk);
2)依据各个聚类中心对象,即对象的均值来计算出与它距离最近的聚类中心,并将对象向聚类中心做以分配。
3)对各个聚类的均值做二次计算:
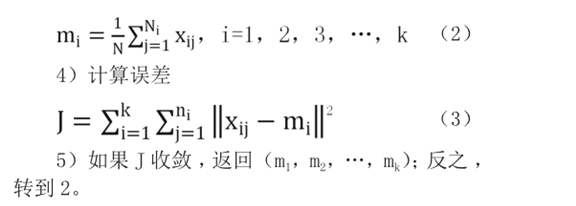
K-means方法是比较快捷和简单的,不过初始聚类中心和最佳聚类数也会影响到聚类结果。
1.2.2 ISODATA方法
ISODATA(Iterative Selforganizing Data Analysis),又叫作迭代自组织数据分析。它是在先验不足的情况下,通过给出一个初始聚类,然后再判断其是否达标,再利用迭代法反复调整,最后得出一个准确的聚类。其采用以下步骤:
1)选择初始值,设置聚类分析控制参数。可以运用各种参数指标,按照指标,将所有模式标本向各个聚类中心进行分配。
2)对各类中全部的样本的距离指标函数进行计算。
3)依据要求,对前一次所得到的聚类集进行分裂,并做并合处理,从而计算出新的聚类中心和分类集。
4)再次做迭代运算,对各项指标进行计算,以判断结果是否达标,直至求出最理想的聚类结果。
IOSDATA算法规则十分明确,便于计算机实现,但是要把握好迭代的次数,防止出现分类不到位的现象。
2 谱聚类方法
谱聚类算法是依据谱图理论所设计的高性能聚类方法。它是基于以下原理:假设{x1,x2,…,xn}代表n个聚类样本,图G=(V,E)可用于表示数据之间的关系,其中V代表顶点集。E代表连接任何两点边的集合。在图中,每个样本xi都可作为顶点,两顶点间的关联性Wij可通过xi与xj相连边的权值来表示。权值矩阵度量图G中,每个顶点间的相似性共同构成相似矩阵,记作W。为了实现图的划分,需要在空中优化某一准则,使同一类的点差别较小,不同类的点差别较大。通常准则函数的优化问题可以通过求解相似矩阵的特征值和特征向量来解决,通过分解相似矩阵的特征值,得到原有的数据集的谱映射,再利用聚类划分算法去计算映射得到的新样本空间,最终得到分类结果。该聚类算法仅与样本点的个数有关,而数据的维数对其没有影响。并且,其对聚类数据样本空间的形状没有特殊要求,容易得到最优解。
3 新型的分类方法
3.1 支持向量机分类法
支持向量机(Support Vector Machine,SVM)是新的分类方法,由Vapnic等人所设计,以统计学理论为基础。近年来,在图像识别中,支持向量机已得到应用,这和中方法的工作机理是,先设计出最佳的线性超平面,最大化它的正与反例间的隔离边缘,从而实现超平面的寻找算法的最优解。SVM作为一种高维的监督分类方法,它是有着不受休斯效应影响的优势,有着不错的效果。但同时,这种方法也有一定缺陷。首先,最大的问题是核函数的选择缺乏指导性,当针对具体的函数时,选择最佳的核函数是一个比较难的问题,还有就是这个方法的计算量较大。
3.2 最小二乘支持向量机分类法
近些年发展了许多SVM的变形,其中最小二乘SVM将优化问题的约束条件变为等式约束,从而不用花费大量的时间解决二次规划问题,使得分类效率大大提高。其算法表达式为:
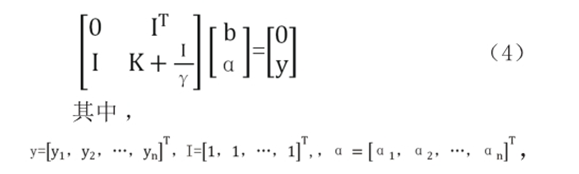
解b,α即可。
最小二乘法SVM在运算的速度上有很大的优势,但其也是有其的缺点。首先来说,最小二乘法会影响到数据的稀疏性,每个数据点都会影响分类模型的构建。然后其估计值的稳定性是低于标准的SVM。同时,在传统SVM基础上,还设计出了拉普拉斯支持向量机(Laplacian Support Vector Machine, LapSVM),它是通过对流形正则化项的添加,无标签和有标签样本的几何信息来构造分类器。LapSVM具备能预测未来测试样本的标签、全局优化、适应性强的特点,更深入的方面就不再赘述。
3.3 决策树分类法
决策树分类法是一种很典型的分类方法,这种分类方法对数据的准备没有太多太高的要求,只是有时需要做比较多的预处理,分类的速度很快。其分类过程分为两步:
1)构建决策树模型。分两步进行,一是建树;二是剪枝。建树是利用递归过程来完成的,最后要形成一棵树;剪枝的目的在于降低训练集杂声造成影响。
2)使用已生成的决策树来对输入的数据进行分类。对待测样本的属性值从根节点依次测试和记录,直到某个节点,从而找到待测样本的属性值。
